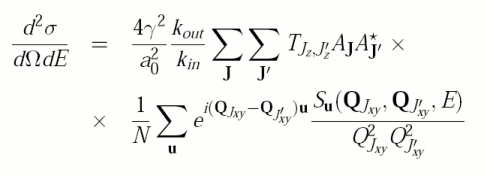| HOME |
| What is CHIRALTEM |
| 2nd CHIRALTEM workshop |
|
Partner: - Vienna - Regensburg - |
| Publications |
|
|

|
First principles calculations of the dichroic effect in the transmission electron microscope Within the first Born approximation the differential
scattering crossection is given by the formula The problem of the calculation of the scattering crosssection can be split into several tasks. The first one is the description of the splitting of the incoming electron beam into Bloch waves. This is calculated according to the dynamical diffraction theory. Equivalent problem is solved for the projection of diffracted beams into the direction defined by the detector position. These tasks can be calculated by knowing the incoming beam energy and the geometry of the experiment (sample orientation, detector orientation). The crucial task, where the input from first-principles codes is needed is the evaluation of the mixed dynamic formfactor S(q,q',E). In our approach S(q,q',E) is evaluated from the knowledge of bandstructure calculated within the density functional theory. Knowledge of eigenfunctions and eigenenergies is necessary for this task. This calculation is implemented using the WIEN2k code.
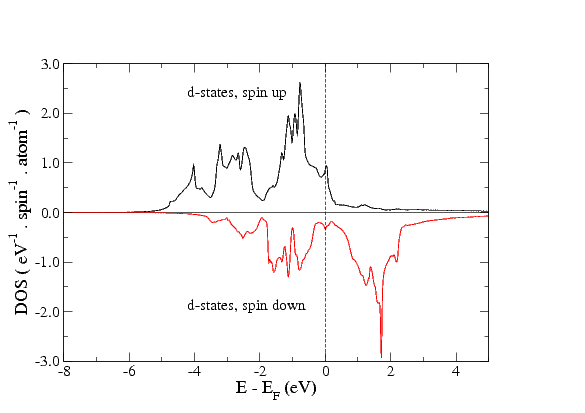
Similarly as in the XMCD the determining features of the electronic structure for observing the dichroism in 3d transition metals are 1) spin-orbit splitting of the initial (core) state 2p into 2p1/2 and 2p3/2; and 2) the exchange splitting of the valence 3d band, i.e. different density of states for spin-up and spin-down electrons (as shown in the figure above for the case of bcc iron).
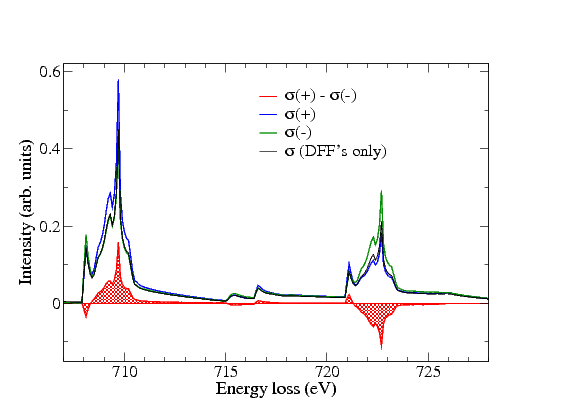
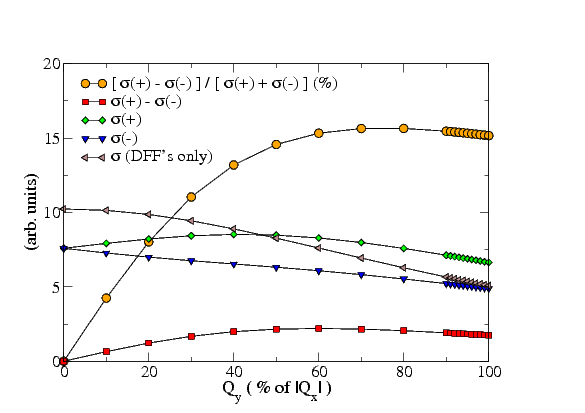
The shape of the 3d DOS to a large extent determines the shape of the L2 and L3 peaks of the scattering crossections (and the dichroism). This is demonstrated on the 2nd figure, where normalized scattering cross-sections and the resulting dichroic effect are displayed (for clarity, these are raw results without any smearings, which of course are present in the real experiment). We have studied the influence of various parameters on the strength of the dichroic effect:
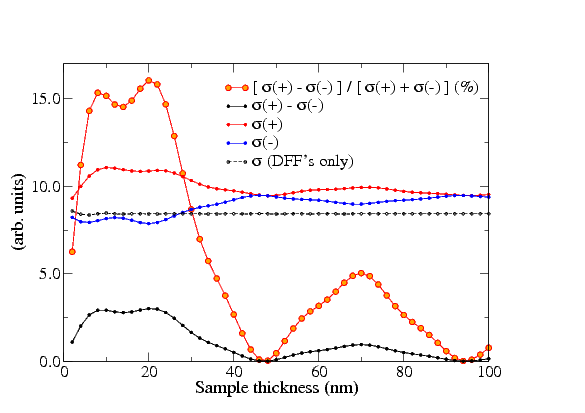
1. The thickness of the sample seems to be a very delicate parameter, beacuse small variations of the thickness can strongly influence the strength of the dichroic effect. Luckily, for iron it seems, that there is a relatively wide interval of thicknesses with a rather strong dichroic signal.
2. The precision of the detector position seems to be a less sensitive parameter. Relatively large displacements along the direction perpendicular to the systematic row of reflections influence the dichroic signal only weakly.
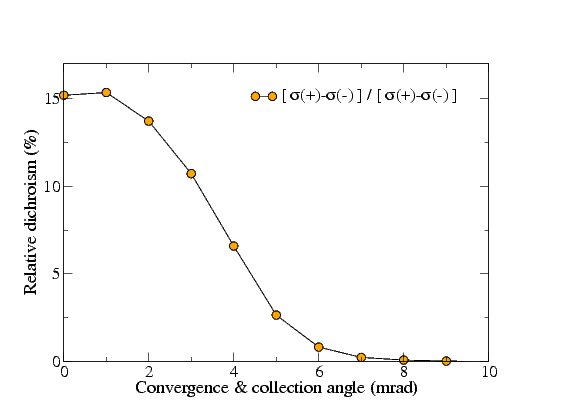
3. All calculations above have been performed
assuming a parallel illumination and point-like detection. In
the last figure we have tested the sensitivity of the dichroic
effect on the size of the convergence and collection angles (set
to be equal in the figure). As one could guess from the previous
figure, where small detector displacements did not degrade the
dichroic signal, the effect of finite angles is modest. |
||